跳转至

块状链表

众所周知，数组可以以 \(O(1)\) 的复杂度查询、修改元素，但删除和插入元素的复杂度是 \(O(n)\) 的；链表恰好相反，插入、删除元素的复杂度为 \(O(1)\)，但查询为 \(O(n)\)。

有没有能以较优复杂度完成插入、删除、查询、修改操作的线性数据结构？

本篇介绍的块状链表就可以。

顾名思义，块状链表运用分块的思想，将数组与链表结合起来。这里引用一张经典的图来展示它大概的样子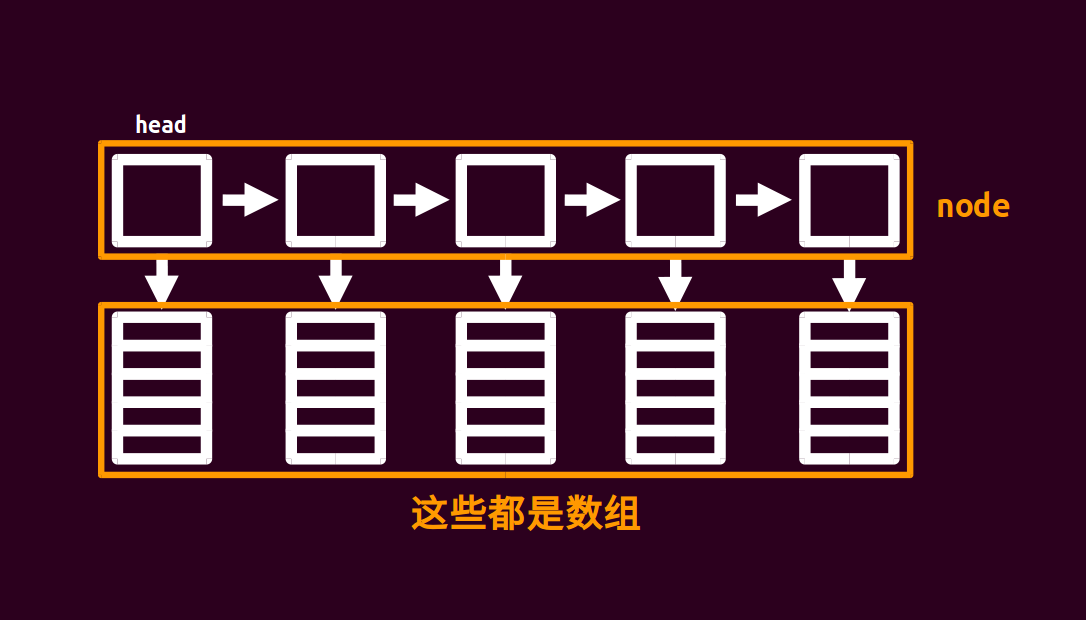： 可以看出块状链表就是以数组为节点（块）的链表。

例一

我们借P4008 [NOI2003] 文本编辑器这道题来理解块状链表的各个操作。

P4008 [NOI2003] 文本编辑器

维护一个字符串，支持在指定位置插入字符串、删除字符串、查询指定长度的连续字串。

内存分配

与正常的链表一样，块状链表中会出现很多新建、删除节点的操作，必须让被删除节点的位置能被新节点再次占用，否则会产生很多空节点，从而使内存巨大。为此我们使用作为内存池的栈 pool[]。

实现 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
void init()
{
    for (int i = 1; i <= mxnum; i++) // 初始化内存池
        pool[i] = i;
    sz[0] = 0;
    nxt[0] = -1; // 标记链表的结尾
}
int new_block()
{
    return pool[++num]; // 取出栈顶空节点
}
void del_block(int x)
{
    pool[num--] = x; // 将被删除的节点压入栈顶
}

合并

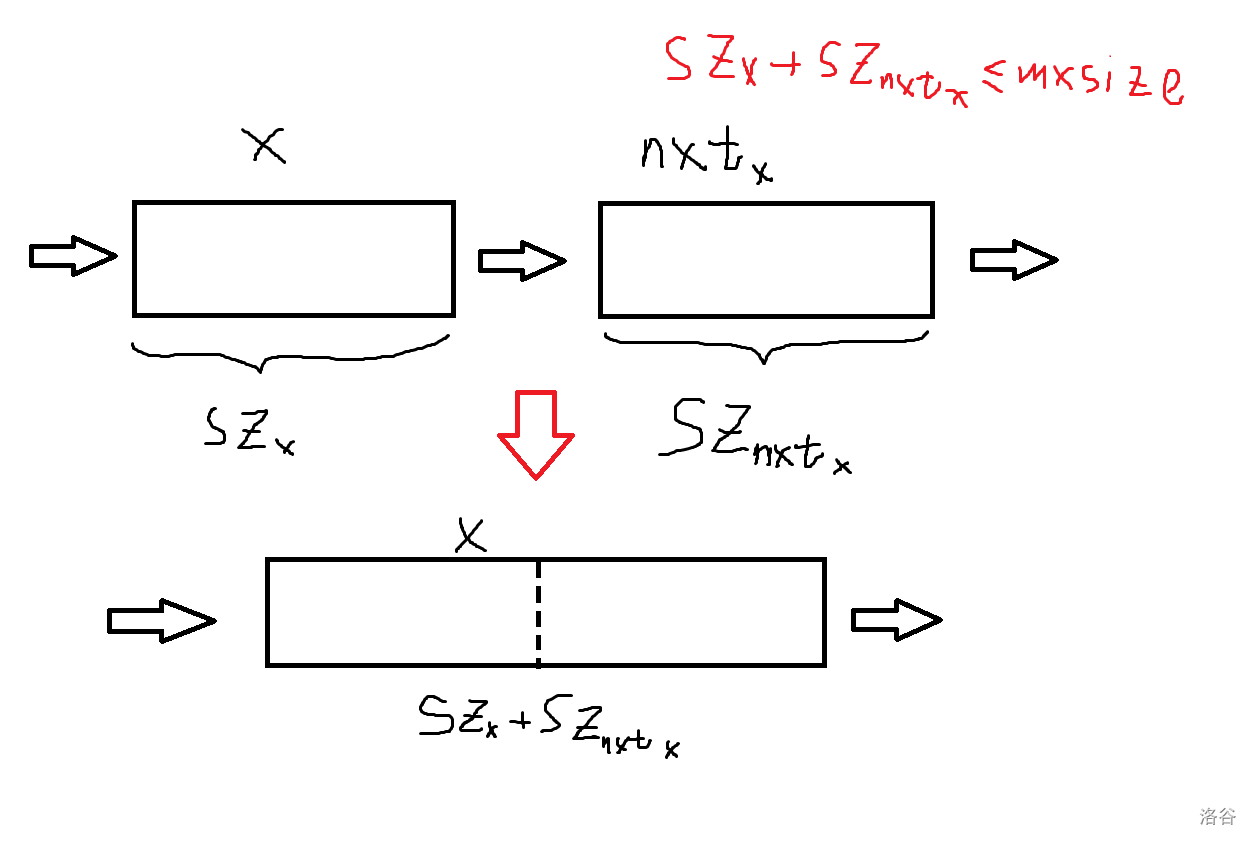
为了保证复杂度，需要同时限制块的总数与最大块长。一个很好的方法是，对于相邻的块，如果他们的长度和不超过最大块长，就将他们合并。

实现 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
void merge(int x, int y)
{
    cpy(dt[x] + sz[x], dt[y], sz[y]); // 手写的复制函数，与memcpy功能相同
    nxt[x] = nxt[y];
    sz[x] += sz[y];
    del_block(y); // 合并后，多出来的块要删掉
}
void maintain() // 遍历整个链表，合并所有可以合并的相邻块
{
    for (int x = 0, y = nxt[0]; x != -1; x = nxt[x], y = nxt[x])
        while (y != -1 && sz[x] + sz[y] <= mxsize)
        {
            merge(x, y);
            y = nxt[x];
        }
}

分裂

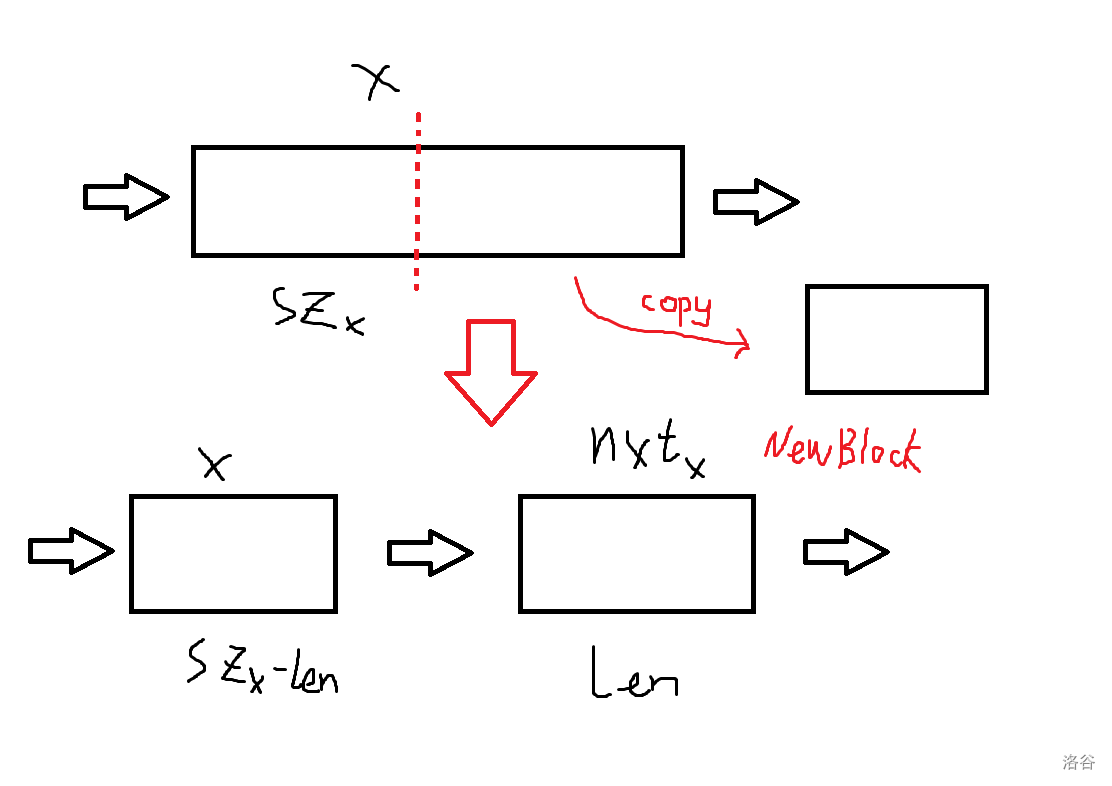
在插入或删除元素时，需要将待操作位置单独分成块，再进行类似链表的插入、删除操作。

实现 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
void update(int x, int y, int len, char *s)
{
    nxt[y] = nxt[x];
    nxt[x] = y;
    sz[y] = len;
    cpy(dt[y], s, len);
}
void split(int x, int pos)
{
    if (x == -1 || pos == sz[x]) return;
    int y = new_block();
    update(x, y, sz[x] - pos, dt[x] + pos); // 新建块
    sz[x] = pos;                            // 记得更新原块长
}

具体操作

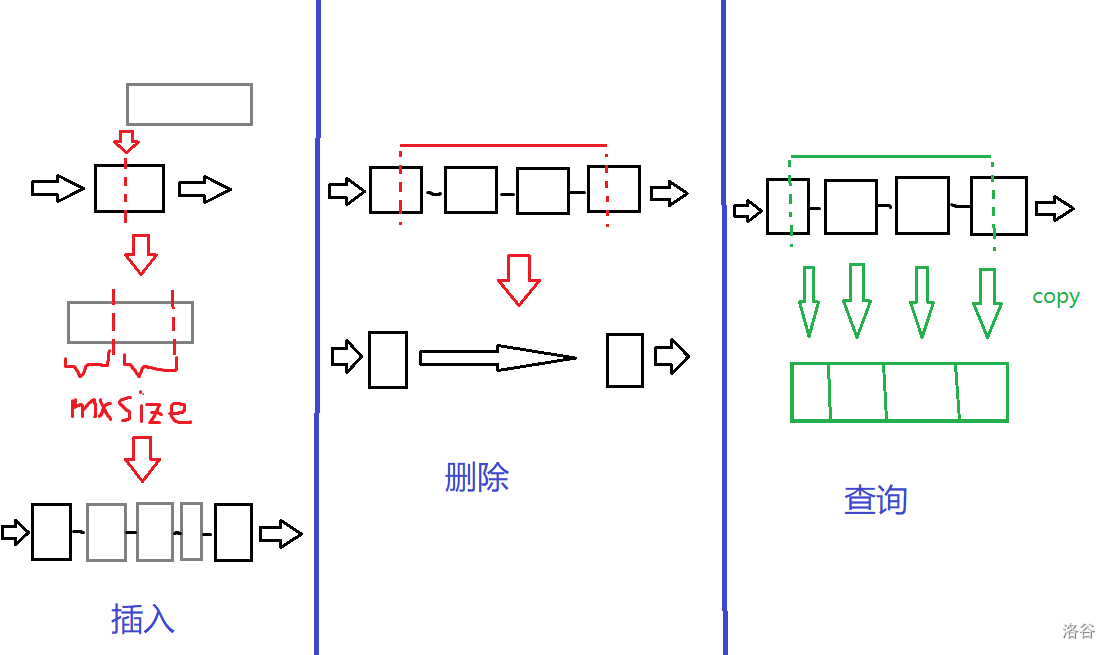
  • 插入：将插入位置的块分裂，把待插入字符串分成长度不超过 \(mxsize\) 的块，依次插入。
  • 删除：将要删除的左右端点的块分裂，删去中间所有块。
  • 查询：将会被查到的所有块复制到答案字符串上。
实现 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
int get_pos(int &pos) // 将输入的位置转换成块上的位置
{
    int x = 0;
    while (x != -1 && pos > sz[x])
    {
        pos -= sz[x];
        x = nxt[x];
    }
    return x;
}
void insert(int pos, int len)
{
    int x = get_pos(pos), y, sum = 0;
    split(x, pos);
    while (sum + mxsize <= len)
    {
        y = new_block();
        update(x, y, mxsize, s + sum);
        sum += mxsize;
        x = y;
    }
    if (len > sum) // 如果切完后还有剩余，尾部自成一块
    {
        y = new_block();
        update(x, y, len - sum, s + sum);
    }
    maintain(); // 插入的左、右端点处可能可以合并，后面删除操作的maintain()同理
}
void erase(int pos, int len)
{
    int x = get_pos(pos), y;
    split(x, pos);
    y = nxt[x];
    while (y != -1 && len > 0)
    {
        if (sz[y] > len) split(y, len);
        len -= sz[y];
        del_block(y);
        y = nxt[y];
    }
    nxt[x] = y; // 记得指向下一块
    maintain();
}
void query(int pos, int len)
{
    int x = get_pos(pos), sum = sz[x] - pos;
    if (len < sum) sum = len;
    cpy(s, dt[x] + pos, sum);
    x = nxt[x];
    while (x != -1 && sum + sz[x] <= len)
    {
        cpy(s + sum, dt[x], sz[x]);
        sum += sz[x];
        x = nxt[x];
    }
    if (x != -1 && len > sum) cpy(s + sum, dt[x], len - sum);
    s[len] = 0; // 标记串的结尾
    printf("%s\n", s);
}

容易得出，当最大块长为 \(\sqrt n\) 时，插入、删除和查询的复杂度均为 \(O(\sqrt n+len)\)。

总体代码

实现 
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
#include <bits/stdc++.h>
using namespace std;
const int N = 1024 * 1024 + 5;
const int mxsize = 3000, mxnum = N * 2 / mxsize + 5; // 要开到N的两倍
int q;
int num, nxt[mxnum], sz[mxnum], pool[mxnum];
char dt[mxnum][mxsize], s[N];
void cpy(char *a, char *b, int len)
{
    for (int i = 0; i < len; i++) *(a + i) = *(b + i);
}
void gets(int len)
{
    for (int i = 0; i < len; i++)
    {
        s[i] = 0;
        while (s[i] < 32 || s[i] > 126) s[i] = getchar();
    }
}
void init()
{
    for (int i = 1; i <= mxnum; i++) // 初始化内存池
        pool[i] = i;
    sz[0] = 0;
    nxt[0] = -1; // 标记链表的结尾
}
int new_block()
{
    return pool[++num]; // 取出栈顶空节点
}
void del_block(int x)
{
    pool[num--] = x; // 将被删除的节点压入栈顶
}
void merge(int x, int y)
{
    cpy(dt[x] + sz[x], dt[y], sz[y]); // 手写的复制函数，与memcpy功能相同
    nxt[x] = nxt[y];
    sz[x] += sz[y];
    del_block(y); // 合并后，多出来的块要删掉
}
void maintain() // 遍历整个链表，合并所有可以合并的相邻块
{
    for (int x = 0, y = nxt[0]; x != -1; x = nxt[x], y = nxt[x])
        while (y != -1 && sz[x] + sz[y] <= mxsize)
        {
            merge(x, y);
            y = nxt[x];
        }
}
void update(int x, int y, int len, char *s)
{
    nxt[y] = nxt[x];
    nxt[x] = y;
    sz[y] = len;
    cpy(dt[y], s, len);
}
void split(int x, int pos)
{
    if (x == -1 || pos == sz[x]) return;
    int y = new_block();
    update(x, y, sz[x] - pos, dt[x] + pos); // 新建块
    sz[x] = pos;                            // 记得更新原块长
}
int get_pos(int &pos) // 将输入的位置转换成块上的位置
{
    int x = 0;
    while (x != -1 && pos > sz[x])
    {
        pos -= sz[x];
        x = nxt[x];
    }
    return x;
}
void insert(int pos, int len)
{
    int x = get_pos(pos), y, sum = 0;
    split(x, pos);
    while (sum + mxsize <= len)
    {
        y = new_block();
        update(x, y, mxsize, s + sum);
        sum += mxsize;
        x = y;
    }
    if (len > sum) // 如果切完后还有剩余，尾部自成一块
    {
        y = new_block();
        update(x, y, len - sum, s + sum);
    }
    maintain(); // 插入的左、右端点处可能可以合并，后面删除操作的maintain()同理
}
void erase(int pos, int len)
{
    int x = get_pos(pos), y;
    split(x, pos);
    y = nxt[x];
    while (y != -1 && len > 0)
    {
        if (sz[y] > len) split(y, len);
        len -= sz[y];
        del_block(y);
        y = nxt[y];
    }
    nxt[x] = y; // 记得指向下一块
    maintain();
}
void query(int pos, int len)
{
    int x = get_pos(pos), sum = sz[x] - pos;
    if (len < sum) sum = len;
    cpy(s, dt[x] + pos, sum);
    x = nxt[x];
    while (x != -1 && sum + sz[x] <= len)
    {
        cpy(s + sum, dt[x], sz[x]);
        sum += sz[x];
        x = nxt[x];
    }
    if (x != -1 && len > sum) cpy(s + sum, dt[x], len - sum);
    s[len] = 0; // 标记串的结尾
    printf("%s\n", s);
}
int main(void)
{
    scanf("%d", &q);
    init();
    int pos = 0;
    while (q--)
    {
        char rd[10];
        scanf("%s", rd);
        if (rd[0] == 'M')
            scanf("%d", &pos);
        else if (rd[0] == 'I')
        {
            int len;
            scanf("%d", &len);
            gets(len);
            insert(pos, len);
        }
        else if (rd[0] == 'D')
        {
            int len;
            scanf("%d", &len);
            erase(pos, len);
        }
        else if (rd[0] == 'G')
        {
            int len;
            scanf("%d", &len);
            query(pos, len);
        }
        else if (rd[0] == 'P')
            pos--;
        else if (rd[0] == 'N')
            pos++;
    }
    return 0;
}

例二

P3391 【模板】文艺平衡树

给定一个长度为 \(n\) 的序列 \(a\)，初始 \(a_i=i\)，执行多次区间翻转操作，求操作后序列。

将需要翻转的区间中的所有块顺序翻转，并给每一块打上翻转标记，在合并、分裂时检查标记。

实现 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void rev(int x)
{
    if (tag[x]) reverse(a[x], a[x] + sz[x]);
    tag[x] = 0; // 翻转后取消标记
}
void rotate(int pos, int len)
{
    int x = get_pos(pos);
    split(x, pos);
    int y = nxt[x];
    top = 0;
    while (len > 0)
    {
        if (sz[y] > len) split(y, len);
        len -= sz[y];
        sta[++top] = y;
        tag[y] ^= 1; // 注意这里不能直接=1
        y = nxt[y];
    }
    sta[++top] = x;
    sta[0] = y;
    for (; top >= 1; top--) nxt[sta[top]] = sta[top - 1]; // 反着连接块
    maintain();
}

例三

P2596 [ZJOI2006] 书架

给定一个 \(1 \sim n\) 的排列，操作为将某个数放到最前面、放到最后面或向前、后移动一步，询问 \(s\) 位置的数或数 \(s\) 的位置。

这三种操作都可以视为从排列中删除一个数，再插入一个数。 这道题中比较麻烦的一点是，移动数的操作给定的都是数的值，因此可以给每一个块开一个桶 book[] 以记录其中是否包含某个数，进行移动操作之前先查询位置。

实现 
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
#include <bits/stdc++.h>
using namespace std;
const int N = 405;
int n, m, k;
int a[N][N], sz[N], pool[N], nxt[N], book[N][80005];
void init()
{
    for (int i = 1; i <= N - 5; i++) pool[i] = i;
    nxt[0] = -1;
}
int new_block() { return pool[++k]; }
void del_block(int x)
{
    for (int i = 0; i < sz[x]; i++) book[x][a[x][i]] = 0; // 记得清空book
    pool[k--] = x;
}
void cpy(int *a, int *b, int len)
{
    for (int i = 0; i < len; i++) *(a + i) = *(b + i);
}
void merge(int x, int y)
{
    cpy(a[x] + sz[x], a[y], sz[y]);
    nxt[x] = nxt[y];
    sz[x] += sz[y];
    for (int i = 0; i < sz[y]; i++) book[x][a[y][i]] = 1;
    del_block(y);
}
void maintain()
{
    for (int x = 0, y = nxt[0]; x != -1; x = nxt[x], y = nxt[x])
        while (y != -1 && sz[x] + sz[y] <= 400)
        {
            merge(x, y);
            y = nxt[x];
        }
}
void update(int x, int y, int len, int *c)
{
    nxt[y] = nxt[x];
    nxt[x] = y;
    sz[y] = len;
    cpy(a[y], c, len);
    for (int i = 0; i < sz[y]; i++) book[y][a[y][i]] = 1;
}
void split(int x, int pos)
{
    if (x == -1 || pos == sz[x]) return;
    int y = new_block();
    update(x, y, sz[x] - pos, a[x] + pos);
    sz[x] = pos;
    for (int i = 0; i < sz[y]; i++) book[x][a[y][i]] = 0;
}
int get_pos(int &pos)
{
    int x = 0;
    while (x != -1 && pos > sz[x])
    {
        pos -= sz[x];
        x = nxt[x];
    }
    return x;
}
void insert(int pos, int num)
{
    int x = get_pos(pos);
    split(x, pos);
    int y = new_block();
    update(x, y, 1, &num);
    maintain();
}
void remove(int pos)
{
    int x = get_pos(pos);
    split(x, pos);
    int y = nxt[x];
    split(y, 1);
    nxt[x] = nxt[y];
    del_block(y);
    maintain();
}
int query(int pos)
{
    int x = get_pos(pos);
    return a[x][pos - 1];
}
int askk(int id)
{
    int x = 0, num = 0;
    while (!book[x][id])
    {
        num += sz[x];
        x = nxt[x];
    } // 跳到包含id的块
    for (int i = 0; i < sz[x]; i++, num++)
        if (a[x][i] == id) // 找到id具体位置
            return num;
}
void top(int id)
{
    if (askk(id) != 0) // 判断边界
    {
        remove(askk(id));
        insert(0, id);
    }
}
void bottom(int id)
{
    if (askk(id) != n - 1)
    {
        remove(askk(id));
        insert(n - 1, id);
    }
}
void step(int id, int t)
{
    if (!t) return;
    int pos = askk(id);
    if (t == 1)
        if (pos != n - 1)
        {
            remove(pos);
            insert(pos + 1, id);
        }
    if (t == -1)
        if (pos != 0)
        {
            remove(pos);
            insert(pos - 1, id);
        }
}
int main(void)
{
    scanf("%d%d", &n, &m);
    init();
    for (int i = 1; i <= n; i++)
    {
        int x;
        scanf("%d", &x);
        insert(i - 1, x);
    }
    for (int i = 1; i <= m; i++)
    {
        char c[10];
        int s, t;
        scanf("%s%d", c, &s);
        if (c[0] == 'T')
            top(s);
        else if (c[0] == 'B')
            bottom(s);
        else if (c[0] == 'I')
        {
            scanf("%d", &t);
            step(s, t);
        }
        else if (c[0] == 'A')
            printf("%d\n", askk(s));
        else if (c[0] == 'Q')
            printf("%d\n", query(s));
    }
    return 0;
}