跳转至

回滚莫队

简介

有些题目在区间转移时，可能会出现增加或者删除无法实现的问题。在只有增加不可实现或者只有删除不可实现的时候，就可以使用回滚莫队在 \(O(n \sqrt m)\) 的时间内解决问题。

形式

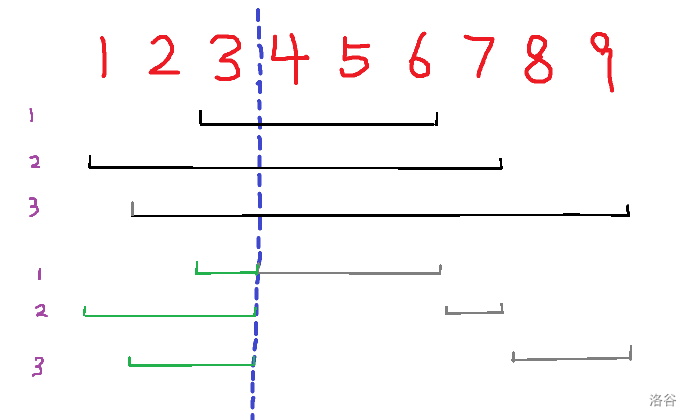
第一步还是将询问的区间按左端点所在块分组，每组内按右端点排序。 实现时对每组单独处理，以左端点所在块右端点（蓝色虚线）为界线。

  • 若左右区间在同一块内，直接暴力计算。
  • 在界线右边的区间（灰色线）的右端点单调不降，可以顺着遍历每个位置。
  • 在界限左边的区间（绿色线）的左端点无序，每次都需要重新遍历，答案在右边的基础上贡献。

复杂度证明

设分块大小为 \(b\) :

  • 对于左右区间在同一块内的询问，每次计算复杂度 \(O(b)\)；
  • 对于界线左边的区间，每次只会在左端点所在块内计算，复杂度 \(O(b)\)；
  • 对于界限右边的区间，在每一组内顺着遍历，最多 \(n\) 次，而有 \(\frac{n}{d}\) 组。

总复杂度为 \(O(mb+\frac{n^2}{d})\)， \(b=\frac{n}{\sqrt{m}}\) 时最优，为 \(O(n\sqrt{m})\)。

例题

不删除莫队

P5906 【模板】回滚莫队&不删除莫队

给定一个序列，多次询问一段区间 \([l,r]\)，求区间中相同的数的最远间隔距离。 序列中两个元素的间隔距离指的是两个元素下标差的绝对值。

对于 \(40\%\) 的数据，满足 \(1\leq a_i \leq 400\)， \(1\leq n,m\leq 60000\)。 对于 \(100\%\) 的数据，满足 \(1\leq n,m\leq 2\cdot 10^5\)， \(1\leq a_i\leq 2\cdot 10^9\)。

按上述方法实现就行，详细请看代码注释。

实现 
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
#include <bits/stdc++.h>
using namespace std;
#define N 200005
int n, m, q, a[N], tot, top, ans[N];
// 一个块的左端点、右端点和某点所在块
int l[505], r[505], to[N];
// 界线右边区间对应数的最小、最大下标 和界线左边区间对应数的最小、最大下标
int l1[N], r1[N], l2[N], r2[N];
// 当前界限右边的答案和总区间的答案
int now;
pair<int, int> p[N];
struct node
{
    int l, r, id;
} st[N];
vector<node> b[505];
// 求l、r和to
void init()
{
    m = sqrt(n);
    for (int i = 1; i <= m; i++)
    {
        l[i] = r[i - 1] + 1;
        r[i] = l[i] + m - 1;
    }
    if (r[m] < n)
    {
        m++;
        l[m] = r[m - 1] + 1;
        r[m] = n;
    }
    for (int i = 1; i <= m; i++)
        for (int j = l[i]; j <= r[i]; j++)
            to[j] = i;
}
bool cmp(node i, node j)
{
    return i.r < j.r;
}
int main(void)
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        p[i] = {a[i], i};
    }
    // 离散化
    sort(p + 1, p + 1 + n);
    for (int i = 1; i <= n; i++)
    {
        if (p[i].first != p[i - 1].first)
            tot++;
        a[p[i].second] = tot;
    }
    init();
    scanf("%d", &q);
    for (int i = 1; i <= q; i++)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        b[to[x]].push_back({x, y, i});
    }
    for (int i = 1; i <= m; i++)
        sort(b[i].begin(), b[i].end(), cmp);
    // 如果像普通莫队那样直接遍历整个q每次都需要判断是否在新的组内，比较麻烦
    // 可为每组开一个vector，对其分开计算
    for (int i = 1; i <= m; i++)
    {
        int len = b[i].size();
        if (!len)
            continue;
        // 这里的l1得赋较大值，否则后面求min(l1,l2)时会算错
        memset(l1, 0x3f, sizeof(l1));
        memset(r1, 0, sizeof(r1));
        int x = r[to[b[i][0].l]] + 1, y = x - 1;
        now = 0;
        for (int j = 0; j < len; j++)
        {
            // 在同一块内暴力算
            if (to[b[i][j].l] == to[b[i][j].r])
            {
                for (int k = b[i][j].l; k <= b[i][j].r; k++)
                {
                    if (!l2[a[k]])
                        l2[a[k]] = k;
                    r2[a[k]] = k;
                    ans[b[i][j].id] = max(ans[b[i][j].id], r2[a[k]] - l2[a[k]]);
                }
                // 复原时不能memset
                for (int k = b[i][j].l; k <= b[i][j].r; k++)
                    l2[a[k]] = r2[a[k]] = 0;
                continue;
            }
            // 算界线右边的
            for (int k = y + 1; k <= b[i][j].r; k++)
            {
                if (l1[a[k]] == l1[0])
                    l1[a[k]] = k;
                r1[a[k]] = k;
                now = max(now, r1[a[k]] - l1[a[k]]);
            }
            ans[b[i][j].id] = now;
            top = 0;
            // 算界线左边的
            for (int k = x - 1; k >= b[i][j].l; k--)
            {
                l2[a[k]] = k;
                if (!r2[a[k]])
                    r2[a[k]] = k;
                ans[b[i][j].id] = max(ans[b[i][j].id], max(r1[a[k]], r2[a[k]]) - min(l1[a[k]], l2[a[k]]));
            }
            // 复原
            for (int k = x - 1; k >= b[i][j].l; k--)
                l2[a[k]] = r2[a[k]] = 0;
            // 右指针向右跳
            y = b[i][j].r;
        }
    }
    for (int i = 1; i <= q; i++)
        printf("%d\n", ans[i]);
    return 0;
}

不增加莫队

P4137 Rmq Problem / mex

有一个长度为 \(n\) 的数组 \(\{a_1,a_2,\ldots,a_n\}\)。 \(m\) 次询问，每次询问一个区间内最小没有出现过的自然数。

对于 \(30\%\) 的数据： \(1\leq n,m\leq 1000\)。 对于 \(100\%\) 的数据： \(1\leq n,m\leq 2\times {10}^5\)， \(1\leq l\leq r\leq n\)， \(0\leq a_i\leq 2\times 10^5\)。

一个集合内最小没有出现过的自然数通常被称为mex。

如果连续插入数，难以维护mex。

容易发现，如果已知mex与一个集合，每次删除其中的数，则mex的变化只会有两种可能：

  • 若当前要删的数 \(x\) 只剩一个，并且 \(x<mex\)，则删后 \(mex\) 变为 \(x\) ;
  • 否则，\(mex\) 不变。

因此也可以用回滚莫队实现，对于每一组内按右端点降序排序，先求出其左侧所在块的左端点到最大右端点的mex，再考虑每次删去一个数时能否更新的mex。

实现 
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
#include <bits/stdc++.h>
using namespace std;
int n, m, q, a[200005], l[505], r[505], to[200005], flag1[200005], flag2[200005], now, ans[200005];
struct node
{
    int l, r, id;
} b[200005];
void init()
{
    m = sqrt(n);
    for (int i = 1; i <= m; i++)
    {
        l[i] = r[i - 1] + 1;
        r[i] = l[i] + m - 1;
    }
    if (r[m] < n)
    {
        m++;
        l[m] = r[m - 1] + 1;
        r[m] = n;
    }
    for (int i = 1; i <= m; i++)
        for (int j = l[i]; j <= r[i]; j++)
            to[j] = i;
}
bool cmp(node i, node j)
{
    if (to[i.l] == to[j.l])
        return i.r > j.r;
    return to[i.l] < to[j.l];
}
int main(void)
{
    scanf("%d%d", &n, &q);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    for (int i = 1; i <= q; i++)
    {
        scanf("%d%d", &b[i].l, &b[i].r);
        b[i].id = i;
    }
    init();
    sort(b + 1, b + 1 + q, cmp);
    int x = 0, y = 0;
    // 这里也可以用上一题的写法，懒得改了QwQ
    for (int i = 1; i <= q; i++)
    {
        // 在同一块内暴力算
        if (to[b[i].l] == to[b[i].r])
        {
            for (int j = b[i].l; j <= b[i].r; j++)
                flag2[a[j]] = 1;
            ans[b[i].id] = n;
            if (!flag2[0])
                ans[b[i].id] = 0;
            for (int j = b[i].l; j <= b[i].r; j++)
                if (!flag2[a[j] + 1])
                    ans[b[i].id] = min(ans[b[i].id], a[j] + 1);
            // 复原
            for (int j = b[i].l; j <= b[i].r; j++)
                flag2[a[j]] = 0;
            continue;
        }
        // 如果这次询问和上次不在一组
        if (to[b[i].l] != to[x])
        {
            for (int j = l[to[x]]; j <= y; j++)
                flag1[a[j]] = 0;
            now = n;
            for (int j = l[to[b[i].l]]; j <= b[i].r; j++)
                flag1[a[j]]++;
            // 暴力算mex
            for (int j = 0; j < n; j++)
                if (!flag1[j])
                {
                    now = j;
                    break;
                }
            x = b[i].l;
            y = b[i].r;
        }
        // 减右边的
        for (int j = y; j > b[i].r; j--)
        {
            flag1[a[j]]--;
            if (!flag1[a[j]])
                now = min(now, a[j]);
        }
        ans[b[i].id] = now;
        // 减左边的
        for (int j = l[to[b[i].l]]; j < b[i].l; j++)
        {
            flag1[a[j]]--;
            if (!flag1[a[j]])
                ans[b[i].id] = min(ans[b[i].id], a[j]);
        }
        // 复原
        for (int j = l[to[b[i].l]]; j < b[i].l; j++)
            flag1[a[j]]++;
        x = b[i].l;
        y = b[i].r;
    }
    for (int i = 1; i <= q; i++)
        printf("%d\n", ans[i]);
    return 0;
}