爬山算法
爬山算法是一种局部择优的方法,采用启发式方法,是对深度优先搜索的一种改进,它利用反馈信息帮助生成解的决策。——Oi Wiki
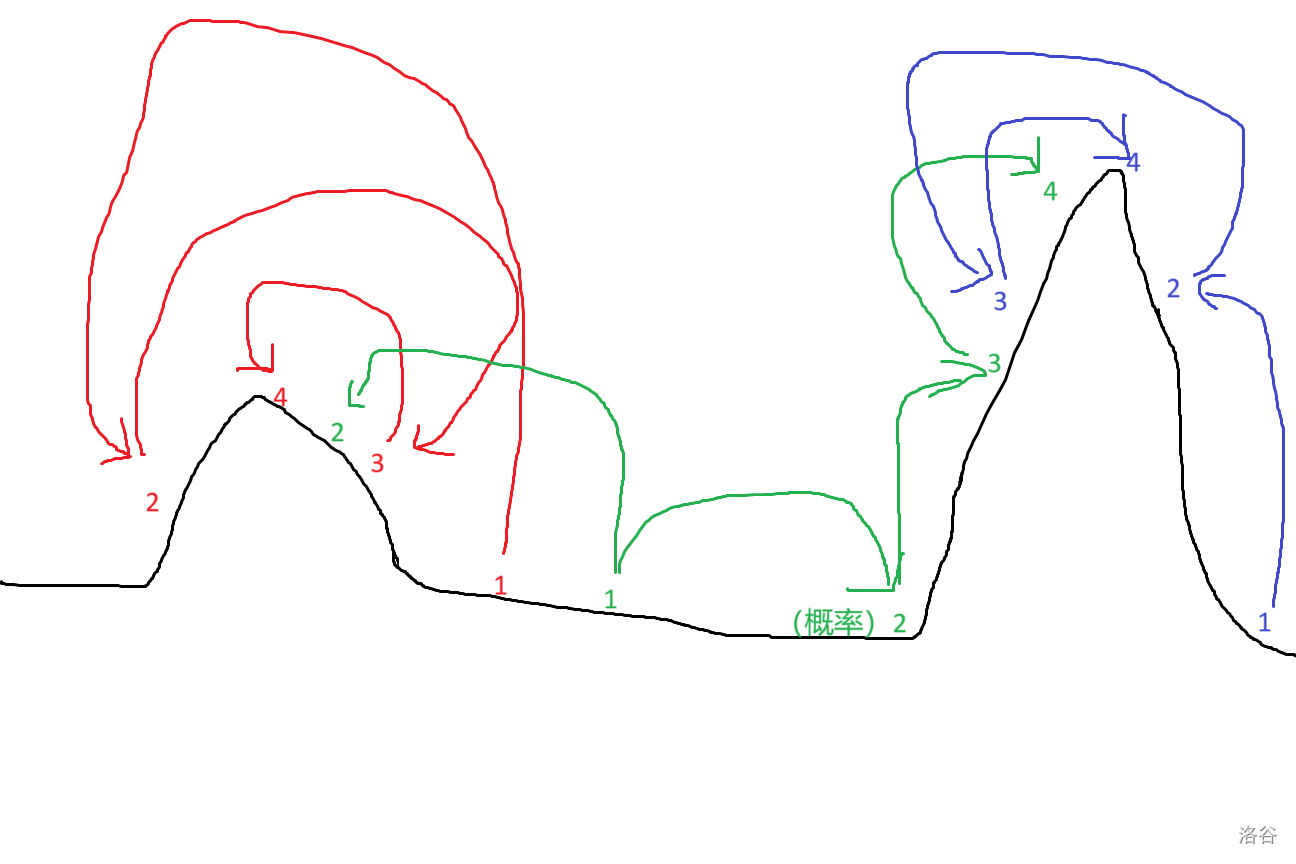
具体来讲,爬山算法的流程就像一只喝醉了的兔子在山上跳,它每次都会朝它认为更高的地方跳。在跳的过程中,兔子会越来越谨慎(即在水平方向上每次跳的距离比前一次短一些)。
下图中蓝色部分能体现这一过程。注意到在 \(2 \rightarrow 3\) 的过程中兔子越过了山顶,但没有关系,随着它跳动距离的减少,它会越来越接近山顶。
例题
P4035 [JSOI2008] 球形空间产生器
给出 \(n\) 维空间中,在一 \(n\) 维球体上的 \(n+1\) 个点坐标,求球心坐标。
讲解引用Oi-Wiki上的:
- 初始化球心为各个给定点的重心(即其各维坐标均为所有给定点对应维度坐标的平均值),以减少枚举量。
- 对于当前的球心,求出每个已知点到这个球心欧氏距离的平均值。
- 遍历所有已知点。记录一个改变值 \(cans\)(分开每一维度记录)对于每一个点的欧氏距离,如果大于平均值,就把改变值加上差值,否则减去。实际上并不用判断这个大小问题,只要不考虑绝对值,直接用坐标计算即可。这个过程可以形象地转化成一个新的球心,在空间里推来推去,碰到太远的点就往点的方向拉一点,碰到太近的点就往点的反方向推一点。
- 将我们记录的 \(cans\) 乘上温度,更新球心,回到步骤 2
- 在温度小于某个给定阈值的时候结束。
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38 | #include <bits/stdc++.h>
using namespace std;
int n;
double spot[15][15], ans[15], dis[15], cans[15];
void check()
{
double sum = 0;
for (int i = 1; i <= n + 1; i++)
{
dis[i] = cans[i] = 0;
for (int j = 1; j <= n; j++)
dis[i] += (spot[i][j] - ans[j]) * (spot[i][j] - ans[j]);
dis[i] = sqrt(dis[i]);
sum += dis[i];
}
sum /= (n + 1);
for (int i = 1; i <= n + 1; i++)
for (int j = 1; j <= n; j++)
cans[j] += (dis[i] - sum) * (spot[i][j] - ans[j]) / sum;
}
int main(void)
{
scanf("%d", &n);
for (int i = 1; i <= n + 1; i++)
for (int j = 1; j <= n; j++)
{
scanf("%lf", &spot[i][j]);
ans[j] += spot[i][j];
}
for (int i = 1; i <= n; i++) ans[i] /= (n + 1);
for (double t = 10001; t >= 0.0001; t *= 0.99995)
{
check();
for (int i = 1; i <= n; i++) ans[i] += cans[i] * t;
}
for (int i = 1; i <= n; i++) printf("%.3lf ", ans[i]);
return 0;
}
|
劣势
如上图中红色部分所示,当有多座山时,兔子最终到达的山顶可能不是最高的。
这也就意味着在目标函数不是单峰函数时,爬山算法容易陷入局部最优解。
