跳转至

线段树分治

引入

线段树分治并不是什么线段树上的骚操作，而是巧妙地利用线段树的思想对时间建树，并以此将一类删除操作用撤销操作取而代之。

例题

P5787 二分图 /【模板】线段树分治

神犇有一个 \(n\) 个节点的图。

因为神犇是神犇，所以在 \(k\) 时间内有 \(m\) 条边会出现后消失。

神犇要求出每一时间段内这个图是否是二分图。

\(n,k = 10^5\)， \(m = 2\times 10^5\)。 \(1 \le x,y \le n\)， \(0 \le l \le r \le k\)。

视频讲解（来源：董晓算法）

先要介绍一下判断二分图的另一种方法：扩展域并查集。

扩展域并查集

因为相连的点在二分图上属不同的集合，因此，每次加一条边 \((u, v)\) 时，我们建立两个反点 \((u', v') = (u + N, v + N)\)，并合并 \(u\) 和 \(v'\)， \(v\) 和 \(u'\) 所在的集合。

那么非常显然，如果正点和反点在同一集合内，那就不是二分图。

我们以时间为元素单位建立一棵线段树。

记边 \((u, v)\) 的存在时间是 \([s, t]\)，我们在线段树上 \([s, t]\) 的区间加入这条边，这里我们采用标记永久化的思想，不去下传边。

然后我们考虑遍历这棵树，每次到一个节点的时候加入所有的边，并且一路判断是否是二分图。

这里我们就会发现我们不需要删除操作了，而是换成了回溯的时候做撤销操作。

并查集的撤销是简单的，我们只需要记录每一次合并操作，然后撤销的时候一步步回退即可。

这里我们不能使用路径压缩，那样会导致大量的赋值操作，我们用按秩合并，我们每次合并的时候，将深度低的集合合并到深度高的，注意维护深度。

实现 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
const int MAXN = 1e5 + 10, MAXV = MAXN << 2, MAXM = 2e5 + 10;
#define mid (((l) + (r)) >> 1)
#define ls ((x) << 1)
#define rs ((x) << 1 | 1)
struct edge
{
    int u, v;
} e[MAXM];
// fy -> fx
struct node
{
    int fx, fy;
    bool added;
};
vector<int> tr[MAXV];
stack<node> stk;
int f[MAXN * 2], h[MAXN * 2], n, m, k;
inline int getf(int x)
{
    while (x != f[x]) x = f[x];
    return x;
}
inline void merge(int x, int y)
{
    x = getf(x), y = getf(y);
    if (h[x] < h[y]) swap(x, y);
    f[y] = f[x];
    stk.push({x, y, h[y] == h[x]});
    if (h[y] == h[x]) h[x]++;
}
inline void del()
{
    auto [fx, fy, added] = stk.top();
    stk.pop();
    h[fx] -= added;
    f[fy] = fy;
}
void update(int x, int l, int r, int pl, int pr, int v)
{
    if (pl <= l && r <= pr) return tr[x].push_back(v);
    if (pl <= mid) update(ls, l, mid, pl, pr, v);
    if (mid < pr) update(rs, mid + 1, r, pl, pr, v);
    return;
}
void solve(int x, int l, int r)
{
    for (int i = 0; i < tr[x].size(); i++)
    {
        int u = e[tr[x][i]].u, v = e[tr[x][i]].v;
        int fu = getf(u), fv = getf(v);
        if (fu == fv)
        {
            for (int j = i; j; j--) del(), del();
            for (int i = l; i <= r; i++) cout << "No\n";
            return;
        }
        merge(u, v + n);
        merge(v, u + n);
    }
    if (l >= r)
        cout << "Yes\n";
    else
        solve(ls, l, mid), solve(rs, mid + 1, r);
    for (int i = tr[x].size(); i; i--) del(), del();
}
int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n >> m >> k;
    for (int i = 1; i <= n * 2; i++) f[i] = i, h[i] = 1;
    for (int l, r, i = 1; i <= m; i++)
    {
        cin >> e[i].u >> e[i].v >> l >> r;
        update(1, 1, k, l + 1, r, i);
    }
    solve(1, 1, k);
    return 0;
}
P4219 [BJOI2014] 大融合

小强要在 \(N\) 个孤立的星球上建立起一套通信系统。这套通信系统就是连接 \(N\) 个点的一个树。

这个树的边是一条一条添加上去的。

在某个时刻，一条边的负载就是它所在的当前能够联通的树上路过它的简单路径的数量。

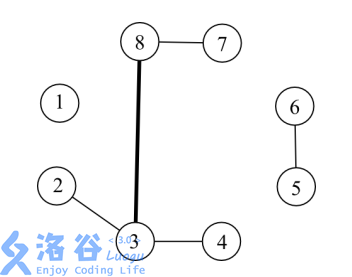
例如，在上图中，现在一共有了 \(5\) 条边。其中，\((3,8)\) 这条边的负载是 \(6\)，因为有六条简单路径 \(2-3-8\) , \(2-3-8-7\) , \(3-8,3-8-7\) , \(4-3-8\) , \(4-3-8-7\) 路过了 \((3,8)\)。

现在，你的任务就是随着边的添加，动态的回答小强对于某些边的负载的询问。

对于所有数据，\(1≤N,Q≤10^5\)

分析

边 \((u, v)\) 的负载就是删去边 \((u, v)\) 后 \(u\) 和 \(v\) 所在连通块大小 \(-1\)。

我们利用Hash压缩边，记录一下并查集每个集合的大小，然后就没有了。

实现 
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
#define mid ((l + r) >> 1)
#define ls ((x) << 1)
#define rs ((x) << 1 | 1)
const int MAXN = 1e5 + 10, MAXM = 2e5 + 10, MAXV = MAXM << 2;
inline ll enc(int u, int v)
{
    if (u > v) swap(u, v);
    return 1ll * u * MAXN + v;
}
inline void dec(ll id, int &u, int &v)
{
    u = id / ll(MAXN);
    v = id % ll(MAXN);
}
int n, q;
map<ll, int> edge;
vector<ll> tr[MAXV];
ll qry[MAXM];
struct DSU
{
    int f[MAXN], stktop, dep[MAXN], siz[MAXN];
    struct oper
    {
        int x, y; // f[y] = x, dep[x] += add, siz[x] += siz[y]
        bool add;
    } his[MAXM];
    inline void init(int n)
    {
        stktop = 0;
        for (int i = 1; i <= n; i++) f[i] = i, dep[i] = siz[i] = 1;
    }
    inline int getf(int x)
    {
        while (x != f[x]) x = f[x];
        return x;
    }
    inline void merge(int x, int y)
    {
        x = getf(x), y = getf(y);
        if (x == y) return;
        if (dep[x] < dep[y]) swap(x, y);
        his[++stktop] = {x, y, dep[x] == dep[y]};
        dep[x] += dep[x] == dep[y];
        siz[x] += siz[y];
        f[y] = x;
    }
    inline void back()
    {
        const auto [x, y, add] = his[stktop--];
        dep[x] -= add;
        siz[x] -= siz[y];
        f[y] = y;
    }
    inline int qry(const int x) { return siz[getf(x)]; }
} dsu;
void insert(int x, int l, int r, int pl, int pr, ll v)
{
    if (pl <= l && r <= pr) return tr[x].emplace_back(v), void();
    if (pl <= mid) insert(ls, l, mid, pl, pr, v);
    if (mid < pr) insert(rs, mid + 1, r, pl, pr, v);
}
void solve(int x, int l, int r)
{
    int tp = dsu.stktop;
    for (ll v : tr[x])
    {
        int p, q;
        dec(v, p, q);
        dsu.merge(p, q);
    }
    if (l == r)
    {
        if (qry[l])
        {
            int p, q;
            dec(qry[l], p, q);
            cout << dsu.qry(p) * dsu.qry(q) << endl;
        }
    }
    else
        solve(ls, l, mid), solve(rs, mid + 1, r);
    while (dsu.stktop > tp) dsu.back();
}
int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n >> q;
    dsu.init(n);
    char ch;
    int x, y, tim = 0;
    ll id;
    for (int i = 1; i <= q; i++)
    {
        cin >> ch >> x >> y;
        id = enc(x, y);
        switch (ch)
        {
        case 'A':
            edge[id] = ++tim;
            break;
        case 'Q':
            insert(1, 1, q << 1, edge[id], tim++, id);
            qry[tim] = id;
            edge[id] = ++tim;
            break;
        }
    }
    for (auto [id, t] : edge)
        if (t)
        {
            dec(id, x, y);
            insert(1, 1, q << 1, t, tim, id);
        }
    solve(1, 1, q << 1);
    return 0;
}
P5631 最小mex生成树

给定 \(n\) 个点 \(m\) 条边的无向连通图，边有边权。

设一个自然数集合 \(S\) 的 \(\text{mex}\) 为：最小的、没有出现在 \(S\) 中的自然数。

现在你要求出一个这个图的生成树，使得其边权集合的 \(\text{mex}\) 尽可能小。

  • 对于 \(100\%\) 的数据，\(1\le n \le 10^6\)， \(1\le m \le 2\times 10^6,0\le w \le 10^5\)。

输入数据规模较大，建议使用高效的读入方式。

分析

我们考虑按顺序依次删掉权值为 \(0, 1, 2, 3, \ldots, 10^5\) 的边。

具体的，对于权值为 \(w\) 的边，我们在 \(0\) 时刻添加这条边，在 \(w\) 时刻删去，此后再加回来，联通就是 \(1\) 号节点所在连通块大小为 \(n\)。

那么我们在遍历线段树的时候每到一个叶子节点就检查是否连通，由于我们是按先左再右的顺序遍历的，因此一发现联通就可以输出了。

实现 
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
#define mid ((l + r) >> 1)
#define ls ((x) << 1)
#define rs ((x) << 1 | 1)
const int MAXN = 1e6 + 10, MAXM = 2e6 + 10, MAXV = MAXM << 2, MAXW = 1e5 + 1;
inline ll enc(int u, int v)
{
    if (u > v) swap(u, v);
    return 1ll * u * MAXN + v;
}
inline void dec(ll id, int &u, int &v)
{
    u = id / ll(MAXN);
    v = id % ll(MAXN);
}
int n, m;
vector<ll> tr[MAXV];
struct DSU
{
    int f[MAXN], stktop, dep[MAXN], siz[MAXN];
    struct oper
    {
        int x, y; // f[y] = x, dep[x] += add, siz[x] += siz[y];
        bool add;
    } his[MAXM];
    inline void init()
    {
        stktop = 0;
        for (int i = 1; i <= n; i++) f[i] = i, siz[i] = dep[i] = 1;
    }
    inline int getf(int x)
    {
        while (x != f[x]) x = f[x];
        return x;
    }
    inline void merge(int x, int y)
    {
        x = getf(x), y = getf(y);
        if (x == y) return;
        if (dep[x] < dep[y]) swap(x, y);
        his[++stktop] = {x, y, dep[x] == dep[y]};
        dep[x] += dep[x] == dep[y];
        siz[x] += siz[y];
        f[y] = x;
    }
    inline void back()
    {
        const auto [x, y, add] = his[stktop--];
        dep[x] -= add;
        siz[x] -= siz[y];
        f[y] = y;
    }
    inline bool qry() { return siz[getf(1)] == n; }
} dsu;
void insert(int x, int l, int r, int pl, int pr, ll v)
{
    if (pl <= l && r <= pr) return tr[x].emplace_back(v), void();
    if (pl <= mid) insert(ls, l, mid, pl, pr, v);
    if (mid < pr) insert(rs, mid + 1, r, pl, pr, v);
}
void solve(int x, int l, int r)
{
    int tp = dsu.stktop;
    for (ll v : tr[x])
    {
        int p, q;
        dec(v, p, q);
        dsu.merge(p, q);
    }
    if (l == r)
    {
        if (dsu.qry())
        {
            cout << l;
            exit(0);
        }
    }
    else
        solve(ls, l, mid), solve(rs, mid + 1, r);
    while (dsu.stktop > tp) dsu.back();
}
int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n >> m;
    dsu.init();
    string ch;
    int u, v, w;
    for (int i = 1; i <= m; i++)
    {
        cin >> u >> v >> w;
        if (w) insert(1, 0, MAXW, 0, w - 1, enc(u, v));
        insert(1, 0, MAXW, w + 1, MAXW, enc(u, v));
    }
    solve(1, 0, MAXW);
    return 0;
}

注意到我们转化了删除操作，因此我们可以处理一些 LCT 解决的问题。

P2147 [SDOI2008] 洞穴勘测

辉辉热衷于洞穴勘测。

某天，他按照地图来到了一片被标记为JSZX的洞穴群地区。经过初步勘测，辉辉发现这片区域由 \(n\) 个洞穴（分别编号为 \(1\) 到 \(n\)）以及若干通道组成，并且每条通道连接了恰好两个洞穴。假如两个洞穴可以通过一条或者多条通道按一定顺序连接起来，那么这两个洞穴就是连通的，按顺序连接在一起的这些通道则被称之为这两个洞穴之间的一条路径。 洞穴都十分坚固无法破坏，然而通道不太稳定，时常因为外界影响而发生改变，比如，根据有关仪器的监测结果，\(123\) 号洞穴和 \(127\) 号洞穴之间有时会出现一条通道，有时这条通道又会因为某种稀奇古怪的原因被毁。

辉辉有一台监测仪器可以实时将通道的每一次改变状况在辉辉手边的终端机上显示：

  • 如果监测到洞穴 \(u\) 和洞穴 \(v\) 之间出现了一条通道，终端机上会显示一条指令 Connect u v；

  • 如果监测到洞穴 \(u\) 和洞穴 \(v\) 之间的通道被毁，终端机上会显示一条指令 Destroy u v。

经过长期的艰苦卓绝的手工推算，辉辉发现一个奇怪的现象：无论通道怎么改变，任意时刻任意两个洞穴之间至多只有一条路径。

因而，辉辉坚信这是由于某种本质规律的支配导致的。因而，辉辉更加夜以继日地坚守在终端机之前，试图通过通道的改变情况来研究这条本质规律。 然而，终于有一天，辉辉在堆积成山的演算纸中崩溃了……他把终端机往地面一砸（终端机也足够坚固无法破坏），转而求助于你，说道：“你老兄把这程序写写吧”。

辉辉希望能随时通过终端机发出指令 Query u v，向监测仪询问此时洞穴 \(u\) 和洞穴 \(v\) 是否连通。现在你要为他编写程序回答每一次询问。 已知在第一条指令显示之前，JSZX洞穴群中没有任何通道存在。

\(100\%\) 的数据满足 \(n \leq 10000, m \leq 200000\)。

保证所有 Destroy 指令将摧毁的是一条存在的通道。

本题输入、输出规模比较大，建议c/c++选手使用scanf和printf进行I/O操作以免超时。

实现 
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
#define mid ((l + r) >> 1)
#define ls ((x) << 1)
#define rs ((x) << 1 | 1)
const int MAXN = 1e5 + 10, MAXM = 2e5 + 10, MAXV = MAXM << 2;
inline ll enc(int u, int v)
{
    if (u > v) swap(u, v);
    return 1ll * u * MAXN + v;
}
inline void dec(ll id, int &u, int &v)
{
    u = id / ll(MAXN);
    v = id % ll(MAXN);
}
int n, q;
map<ll, int> edge;
vector<ll> tr[MAXV];
ll qry[MAXM];
struct DSU
{
    int f[MAXN], stktop, dep[MAXN], siz[MAXN];
    struct oper
    {
        int x, y; // f[y] = x, dep[x] += add, siz[x] += siz[y]
        bool add;
    } his[MAXM];
    inline void init(int n)
    {
        stktop = 0;
        for (int i = 1; i <= n; i++) f[i] = i, dep[i] = siz[i] = 1;
    }
    inline int getf(int x)
    {
        while (x != f[x]) x = f[x];
        return x;
    }
    inline void merge(int x, int y)
    {
        x = getf(x), y = getf(y);
        if (x == y) return;
        if (dep[x] < dep[y]) swap(x, y);
        his[++stktop] = {x, y, dep[x] == dep[y]};
        dep[x] += dep[x] == dep[y];
        siz[x] += siz[y];
        f[y] = x;
    }
    inline void back()
    {
        const auto [x, y, add] = his[stktop--];
        dep[x] -= add;
        siz[x] -= siz[y];
        f[y] = y;
    }
    inline int qry(const int x) { return siz[getf(x)]; }
} dsu;
void insert(int x, int l, int r, int pl, int pr, ll v)
{
    if (pl <= l && r <= pr) return tr[x].emplace_back(v), void();
    if (pl <= mid) insert(ls, l, mid, pl, pr, v);
    if (mid < pr) insert(rs, mid + 1, r, pl, pr, v);
}
void solve(int x, int l, int r)
{
    int tp = dsu.stktop;
    for (ll v : tr[x])
    {
        int p, q;
        dec(v, p, q);
        dsu.merge(p, q);
    }
    if (l == r)
    {
        if (qry[l])
        {
            int p, q;
            dec(qry[l], p, q);
            cout << dsu.qry(p) * dsu.qry(q) << endl;
        }
    }
    else
        solve(ls, l, mid), solve(rs, mid + 1, r);
    while (dsu.stktop > tp) dsu.back();
}
int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n >> q;
    dsu.init(n);
    char ch;
    int x, y, tim = 0;
    ll id;
    for (int i = 1; i <= q; i++)
    {
        cin >> ch >> x >> y;
        id = enc(x, y);
        switch (ch)
        {
        case 'A':
            edge[id] = ++tim;
            break;
        case 'Q':
            insert(1, 1, q << 1, edge[id], tim++, id);
            qry[tim] = id;
            edge[id] = ++tim;
            break;
        }
    }
    for (auto [id, t] : edge)
        if (t)
        {
            dec(id, x, y);
            insert(1, 1, q << 1, t, tim, id);
        }
    solve(1, 1, q << 1);
    return 0;
}
P5227 [AHOI2013] 连通图

给定一个无向连通图和若干个小集合，每个小集合包含一些边，对于每个集合，你需要确定将集合中的边删掉后改图是否保持联通。集合间的询问相互独立。

定义一个图为联通的当且仅当对于任意的两个顶点，都存在一条路径连接它们。

\(1\leq n,k\leq 10^5\)， \(1\leq m\leq 2\times 10^5\)， \(1\leq c\leq 4\)。

实现 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e5 + 10, MAXM = 2e5 + 10;
#define mid ((l + r) >> 1)
#define ls ((x) << 1)
#define rs ((x) << 1 | 1)
struct edge
{
    int u, v;
} e[MAXM];
// x <- y
struct node
{
    int x, y;
    bool added;
} oper[MAXM];
vector<int> tr[MAXM << 2];
int f[MAXN], n, m, k, lst[MAXM], siz[MAXN], deep[MAXN], top, c;
inline int getf(int x)
{
    while (x != f[x]) x = f[x];
    return x;
}
inline void merge(int x, int y)
{
    x = getf(x), y = getf(y);
    if (x == y) return;
    if (deep[x] < deep[y]) swap(x, y);
    f[y] = x;
    siz[x] += siz[y];
    oper[++top] = {x, y, deep[x] == deep[y]};
    deep[x] += deep[x] == deep[y];
}
inline void backspace()
{
    auto [x, y, added] = oper[top--];
    f[y] = y;
    siz[x] -= siz[y];
    deep[x] -= added;
}
void update(int x, int l, int r, int pl, int pr, int v)
{
    if (pl <= l && r <= pr)
    {
        tr[x].push_back(v);
        return;
    }
    if (pl <= mid) update(ls, l, mid, pl, pr, v);
    if (mid < pr) update(rs, mid + 1, r, pl, pr, v);
}
void solve(int x, int l, int r)
{
    int ttop = top;
    bool yes = 0;
    for (int i : tr[x]) merge(e[i].u, e[i].v);
    if (siz[getf(1)] == n)
    {
        for (int i = l; i <= r; i++) cout << "Connected\n";
        yes = 1;
    }
    if (!yes)
        if (l == r)
            cout << "Disconnected\n";
        else
            solve(ls, l, mid), solve(rs, mid + 1, r);
    while (top != ttop) backspace();
}
int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= n; i++) deep[i] = siz[i] = 1, f[i] = i;
    for (int i = 1; i <= m; i++) cin >> e[i].u >> e[i].v;
    cin >> k;
    for (int i = 1; i <= k; i++)
    {
        int c, t;
        cin >> c;
        while (c--)
        {
            cin >> t;
            if (lst[t] != i - 1) update(1, 1, k, lst[t] + 1, i - 1, t);
            lst[t] = i;
        }
    }
    for (int i = 1; i <= m; i++)
        if (lst[i] != k) update(1, 1, k, lst[i] + 1, k, i);
    solve(1, 1, k);
    return 0;
}